Globals - Magic swords for storing data. Sparse arrays. Part 3.

In the previous parts (1, 2) we talked about globals as trees. In this article, we will look at them as sparse arrays.

A sparse array - is a type of array where most values assume an identical value.

In practice, you will often see sparse arrays so huge that there is no point in occupying memory with identical elements. Therefore, it makes sense to organize sparse arrays in such a way that memory is not wasted on storing duplicate values.

In some programming languages, sparse arrays are part of the language - for example, in J, MATLAB. In other languages, there are special libraries that let you use them. For C++, those would be Eigen and the like.

Globals are good candidates for implementing sparse arrays for the following reasons:

1. They store values of particular nodes only and do not store undefined ones;
2. The access interface for a node value is extremely similar to what many programming languages offer for accessing an element of a multidimensional array.

    

    

   Set ^a(1, 2, 3)=5
   Write ^a(1, 2, 3)

3. A global is a fairly low-level structure for storing data, which is why globals possess outstanding performance characteristics (hundreds of thousands to dozens of millions of transactions per second depending on hardware, see 1)

Since a global is a persistent structure, it only makes sense to create sparse arrays on their basis in situations where you know in advance that the you will have enough memory for them.

One of the nuances of implementing sparse arrays is the return of a certain value by default if you are addressing an undefined element.

This can be implemented using the $GET function in COS. Let's take a look at a 3-dimensional array in this example.

SET a = $GET(^a(x,y,z), defValue)

So what kind of tasks require sparse arrays and how can globals help you?

Adjacency matrix

Such matrices are used for graph representation:

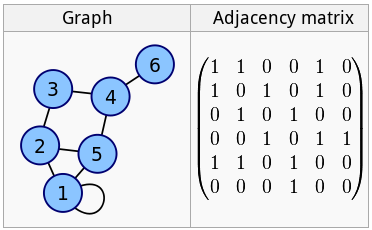
It's obvious that the larger a graph is, the more zeroes there will be in the matrix. If we look at a graph of a social network, for example, and represent it as a matrix or this type, it will mostly consist of zeroes - that is, be a sparse array.

Set ^m(id1, id2) = 1 
Set ^m(id1, id3) = 1 
Set ^m(id1, id4) = 1 
Set ^m(id1) = 3 
Set ^m(id2, id4) = 1 
Set ^m(id2, id5) = 1 
Set ^m(id2) = 2
....

In this example, we will save the adjacency matrix in the ^m global, as well as the number of each node's edges (who's friends with whom and the number of friends).

If the number of elements in the graph does not exceed 29 million (this number is calculated as 8 * maximum string length), there is even a more economical method of storing such matrices - bit strings, since they optimize large gaps in a special way.

Manipulations with bit strings are carried out with the help of the $BIT function.

; setting a bit
SET $BIT(rowID, positionID) = 1
; getting a bit
Write $BIT(rowID, positionID)

Table of FSM switches

Since the graph of FSM switches is a regular graph, the table of FSM switches is essentially the same adjacency matrix we spoke about earlier.

Cellular automata

The most famous cellular automaton - is the "Life" game, where rules (when a cell has many neighbors, it dies) essentially make it a sparse array.

Stephen Wolfram believes that cellular automata are a new field of science. In 2002, he published a 1280-page book called "A New Kind of Science", where he states that achievements in the area of cellular automata are not isolated, but are quite stable and are important for all fields of science.

It has been proved that any algorithm that can be processed by a computer can also be implemented with the help of a cellular automaton. Cellular automata are used for simulating dynamic environments and systems, for solving algorithmic problems and for other purposes.

If we have a huge field and need to register all intermediate states of a cellular automaton, it makes sense to use globals.

Cartography

The first thing that pops in my mind when it comes to using sparse arrays is cartography.

As a rule, maps have lots of empty space. If we imagine that the world map is comprised of large pixels, we'll see that 71% of all Earth's pixels will be occupied by the ocean' a sparse array. And if we only add artificial structures to the map, there will be over 95% of empty space.

Of course, no one stores maps as bitmap arrays, everybody uses vector representation instead.
But what are vector maps? It's some kind of frame along with polylines and polygons.
In essence, it a database of points and relations between them.

One of the most challenging tasks in cartography is the creation of a map of our galaxy carried out by the Gaia telescope. Figuratively speaking, our galaxy is one mammoth sparse array: huge empty spaces with occasional bright spots - stars. It's 99,999999.......% of absolutely empty space. Cache, a database based on globals, was selected for storing the map of our galaxy.

I don't know the exact structure of globals in this project, but I can assume that it's something like this:

Set ^galaxy(b, l, d) = 1; star catalog number, if exists
Set ^galaxy(b, l, d, "name") = "Sun"
Set ^galaxy(b, l, d, "type") = "normal" ; other options may include a black hole, quazar, red_dwarf and such.
Set ^galaxy(b, l, d, "weight") = 14E50
Set ^galaxy(b, l, d, "planetes") = 7
Set ^galaxy(b, l, d, "planetes", 1) = "Mercury"
Set ^galaxy(b, l, d, "planetes", 1, weight) = 1E20
...

Where b, l, d are galactic coordinates: latitude, longitude and distance from the Sun.

The flexible structure of globals allows you store any star and planet characteristics, since global-based databases are scheme-less.

Cache was selected for storing the map of our universe not just because of its flexibility, but also thanks to its ability to quickly save a data thread while concurrently creating index globals for quick search.

If we go back to Earth, globals were used in such map-focused projects OpenStreetMap XAPI and FOSM, a fork of OpenStreetMap.

Just recently at a Caché hackathon, a group of developers implemented Geospatial indexes using this technology. See the article for details.

Implementation of geospatial indexes using globals in OpenStreetMap XAPI

Illustrations were taken from this presentation.

The entire globe is broken into squares, then subsquares, then into more subsquares, and so on. In the end, we get a hierarchical structure that globals were created for.

At any moment, we can instantly request any square or empty it, and all the subsquares will be returned or emptied as well.

A detailed scheme based on globals can be implemented in several ways.

Variant 1:

Set ^m(a, b, a, c, d, a, b,c, d, a, b, a, c, d, a, b,c, d, a, 1) = idPointOne
Set ^m(a, b, a, c, d, a, b,c, d, a, b, a, c, d, a, b,c, d, a, 2) = idPointTwo
...

Variant 2:

Set ^m('abacdabcdabacdabcda', 1) = idPointOne
Set ^m('abacdabcdabacdabcda', 2) = idPointTwo
...

In both cases, it won't be much of a trouble in COS/M to request points located in a square of any level. It will be somewhat easier to clear square segments of space of on any level in the first variant, but this is seldom required.

An example of a low-level square:

And here are some globals from the XAPI project: representation of an index based on globals:

The^way global is used for storing the vertices ofpolylines (roads, small rivers, etc.) and polygons (enclosed areas: buildings, woods, etc.).

A rough classification of the use of sparse arrays in globals.

1. We store the coordinates of some objects and their state (cartography, cellular automata).
2. We store sparse matrices.

In variant 2) when a certain coordinate is requested and there is no value assigned to an element, we need to get the default value of the element of the sparsed array.

Benefits that we get when storing multi-dimensional matrices in globals

Quick deletion and/or selection of segments of space that are multiple of strings, surfaces, cubes, etc. For cases with integer indexes it may be convenient to be able to quickly remove and/or select segments of space that are multiple of strings, surfaces, cubes and such.

The Kill command can delete a standalone element, a string, and even an entire surface. Thanks to the properties of the global, it happens very quickly' a thousand times faster than element-by-element deletion.

The illustration shows a three-dimensional array in global ^a and different types of removals.

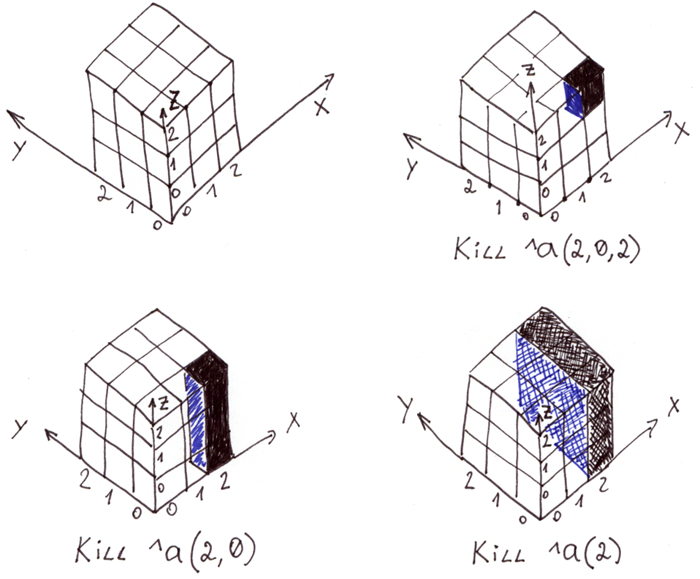
To select segments of space by known indices, you can use the Merge command.

Selection of a matrix column into the Column variable:

; Let's define a three-dimensional 3x3x3 sparse array 
Set ^a(0,0,0)=1,^a(2,2,0)=1,^a(2,0,1)=1,^a(0,2,1)=1,^a(2,2,2)=1,^a(2,1,2)=1
Merge Column = ^a(2,2)
; Let's output the Column variable
Zwrite Column

Output:

Column(0)=1
Column(2)=1

What's interesting is that we got a sparse array in the Column variable that you can address via $GET since default values are not stored there.

Selection of segments of space can also be made with the help of a small program using the $Order function. This comes in especially handy in spaces with with nonquantized indices (cartography).

Conclusion

The realities of today pose new challenges. Graphs can consist of billions of vertices, maps can have billions of points, some may even want to launch their own universe based on cellular automata (1, 2).

When the volume of data in sparse arrays cannot be squeezed into RAM, but you still need to work with them, you should consider implementing such projects using globals and COS.

Thank you for your attention! Looking forward to seeing your questions and requests in the comments section.